Project Presentation

Combat Robot

Impedance and Analysis

In this lab we learned that in order to have a real inductor a resistor has to be added in series. Using a DMM we measured the resistance in our unknown inductor to be 2 ohms. We applied an AC current in order to determine the capacitance but in order to not damage the equipment we added another resistor to limit the current which was measured at 67.6 ohms. We build the circuit. VIN = 2.88V IIN = 42.3 mA

Computation:
Z = V/I = 72.2
Rext + RL + ZLj
Z = sqrt((Rext + RL)^2 + ZL^2)
w = 2(pi)(1000)
72.2^2 =sqrt(68.9^2+ZL^2)     ZL =21.63 ohms = wL    L = 3.44*10^-3
wL = 1/wC    C= 1/w^2L = 7.36*10^-6 H

Vppch1 = 2 mV

Vppch2 = 1.5 V

delta t = 10 ms

There is a phase difference 90

Frequency (Hz)	Vin (V)	Iin  (mA)	Zin (Ω)
100	4.63	19.9	232.7
500	3.21	39.2	81.9
1 k	2.96	40.6	72.9
5 k	2.90	38.6	75.2
10 k	2.96	32.8	90.2

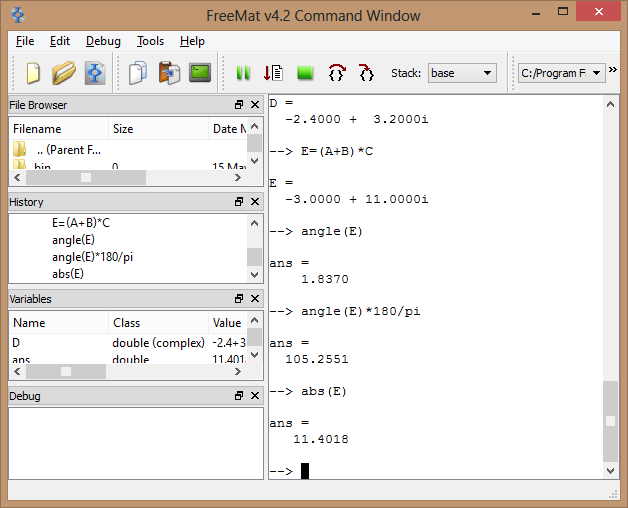
FreeMat Complex numbers

In this lab we learned how to use freemat with complex numbers

Exercise 1

 Exercise 1

Exercise 2

Assignment

MOSFET

In this lab we use a MOSFET to control the voltage across a motor.

We first connect the motor to the MOSFET and a potentiometer.

We observe that the motor does not begin to rotate until around 3.9 V

As we adjust the pot we notice that the motor reacts to the change in voltage that is occurring. It is fairly difficult to make the motor shaft rotate at approximately once per second.

PWM Chopper MOSFET 

We replace the pot with a square wave generator set at 10 Khz. We use the oscilloscope to display the waveform of the motor voltage.

Practice RLC Circuit

Oscilloscope 101

In this lab we practiced using the oscilloscope which will help us measure the voltage and time of a signal based on the wave shape. This instrument will help in future labs.

We first had to get a sign wave to appear on our oscilloscope with a frequency of 5 kHz and amplitude of 5 V. We measured the period to be 210 us, peak to peak amplitude of 10 V, zero to peak of 5 V, and RMS value of 3.53

We then verified these values with the DMM and got VDC = 0 and VAC = 3.36

We then included a DC offset

adding a 2.5 V offset we attained the values    VDC = 2.5 V and VAC = 1.17 V

We then displayed a square function

VDC = 0 V and VAC = 2.6 V

we calculate VAC = sqrt(2.5^2 * 4 * 50ms/ 4 * 50 ms) = 2.5 V

Mystery Signal: After establishing a steady wave function we measured DC = .03V frequency = 133k Hz and peak to peak amp to be .13 V

Capacitor Charging / Discharging

In this lab we observed the relations of charging and discharging a capacitor. The relation we see from our equations is that it will essentially never fully charge or discharge as it exponentially approaches either value. With the given knowledge of capacitors we are to construct a circuit from which we determine the thevin values.

We utilize a 9 V DC power supply and determine that C = 62uF from w = CV^2 / 2. There is a charging interval of about 20s with a resulting stored energy of 2.5 mJ and then discharged in 2 s.

Assuming an ideal capacitance we estimate charging resistance to be 64.5 k ohms

Using V = IR we determine the peak current value to be 0.14 mA and P = IV to determine peak power to be 1.26 mW.

The discharging resistance is estimated to be 6.45 k ohms and the peak discharge current and power are 1.4 mA and 12.6 mW respectively.

We set the power sipply to be 6 V         V measured = 5.707 V

VFinal = Vs (RLeak)/(Rc + RLeak)         RLeak = 1.256 M ohms

Graph of charging capacitor 

 charging took about 20 seconds

Graph of discharging capacito

discharging took about 2 seconds

Questions:

1. Thevenin Values During Charging

RTH = 61.4 k ohms

VTH = 5.707 V

2. Thevenin Values During Disharging

RTH = 6.42 k ohms

VTH = 5.707 V

3. 0.3679 * VF = 3.607 V  this occurs around 4s according to our charging waveform

t=RC    4 = R * 62 uF   R = 64.5 K ohms

Practical Question:

1. E = V^2 C/2 = 160 mJ = 15kV^2  C / 2       C = 1.4 F

2. C||C + C||C + C||C + C||C = 1.4 F

C = .7

OP Amps II

In this lab we further explore operational amplifiers by observing the effects of changing the input and feedback resistors. We began the lab with the first set of values being:

Resistor	Nominal Value	Measured Value
R1	10K Ω	9.79k Ω
R2	100k Ω	95.2k Ω

The current leaving the op-amp is 0.1 mA

After setting up our circuit we recorded the values  for various V in values.

V in Desired	V in actual	V out measured	V RF measured	I op Calculated
0.25 V	0.251 V	2.49 V	2.50 V	0.0263 mA
0.5 V	0.433 V	4.25 V	4.26 V	0.0447 mA
1.0 V	1.192 V	10.76 V	10.79 V	0.113 mA

ICC = 1.01 mA   IEE = -0.91 mA

We see that KCL for the op amp is true
Irail = IEE + ICC = 0.1 mA
Power calculated
PIcc = 12V *1.01 mA = 12.12 mW
PIEE = 12V * (-.91 mA) = -10.92 mW

We then add a 1k resistor to our circuit and remeasure the values when V in = 1.0 V

V in Desired	V out measured	V RF measured	I op calculated	I cc measured	I EE measured
0.93 V	9.39 V	8.99 V	0.094 mA	0.93 mA	-1.04 mA

KCL still holds  Icc + IEE = 0.11 mA
Power calculated

PIcc = 12V *0.93 mA = 11.16 mW
PIEE = 12V * (-1.04 mA) = -12.48 mW


We then reproduce the lab by replacing Rf = 50k ohms which we set with a resistor box.

V in Desired	V out measured	V Rf measured	I op calculated	I cc measured	I EE measured
1.08 V	5.44 V	5.47 V	0.109 mA	0.9 mA	-1.01 mA

The measurements still behave as expected. KCL holds. 

Op Amp 1

  

In this lab we are to have a sensor whose output ranges from 0 to +1V and whose Thevenin output resistance is negligible. the output range must be between 0 and -10V and must draw no more than 1mA from the senseor and the op amp power supplies should be no more than 30 mW.
From our calculations we determined Ri = 1 k ohms and Rf = 10 k ohms
We proceed by determining Rx = 8 * V^2 = 1152 ohms      RY / (RY + RY) * 12 =1     RY = 288 ohms
From this we find that RTH = 230.4 ohms which is at least 20 times smaller than the resistance value of R1

Applying our theoretical results we attain the following

Component Nominal Value Measured Value Power Rating

        Ri                1k ohm      984 ohm            0.25 W

        Rf                10k ohm      9.74 ohm            0.25 W

        Rx                1k ohm      982 ohm            0.25 W

        Ry                     x                    x                         x

        V1                  12 V      12.06 ohm               2 A

        V2                  12 V       12.1 ohm               2 A

Vin           Vout Gain          VRi         IRi           VRf

0.0V          0V             0           0V          0 mA      0

0.25V -2.48V -9.92 .249V .253 mA -2.48 V

0.5V -       4.97V -9.94 .5V         .508 mA -5.01 V

0.76V -7.48V -9.97 .751V .763 mA -7.52 V

1.004V -10.03V -9.98 1.005V 1.02 mA -10.01 V

IV1 = 1.737 mA                            IV2 = 1.276 mA

PV1 = IV1 * V1 = 20.9 mW            PV2 = IV2 * V2 = 15.4 mW

I_Ri = V_in / R_i =1.004 / 984 = 1.02 mA

I_Rf =  V_Rf / R_f  = 10.01 / 9740 = 1.02 mA

From our calculations we see that the power supply constraint of no more than 30 mW is maintianed. In order to reduce the power drawn we should increase the resistor values in a way that the ration Rf/Ri = 10.

PSpice

In this lab we practicing using the program PSpice.

First Circuit

Second Circuit

VTH = 10 V    RTH = 3.33 ohms    IN = 3 A

Maximum Power Transfer

In this lab we verified the Maximum Power Transfer Theorem in a simple series circuit and use the theorem to determine the Thevinin Resistance.

We then build the circuit using a potentiometer and recorded the values of V, R and P from the lowest to highest resistance of the potentiometer.

we then built the following circuit

we followed by using the data we obtained in LoggerPro